What Does It Mean to Say Something Is in Mechanical Equilibrium?

April 02, 2022 Post a Comment

In classical mechanics, a particle is in mechanical equilibrium if the internet force on that particle is zero

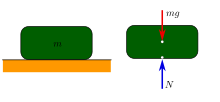
An object resting on a surface and the respective gratuitous trunk diagram showing the forces interim on the object. The normal force N is equal, opposite, and collinear to the gravitational strength mg so the net forcefulness and moment is zero. Consequently, the object is in a state of static mechanical equilibrium.

In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zilch.^[1] ^: 39 By extension, a physical arrangement made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is naught.^[1] ^: 45–46 ^[2]

In addition to defining mechanical equilibrium in terms of force, at that place are many alternative definitions for mechanical equilibrium which are all mathematically equivalent. In terms of momentum, a organization is in equilibrium if the momentum of its parts is all constant. In terms of velocity, the organization is in equilibrium if velocity is abiding. In a rotational mechanical equilibrium the athwart momentum of the object is conserved and the internet torque is zero.^[2] More generally in conservative systems, equilibrium is established at a indicate in configuration space where the gradient of the potential energy with respect to the generalized coordinates is nothing.

If a particle in equilibrium has null velocity, that particle is in static equilibrium.^[3] ^[4] Since all particles in equilibrium accept constant velocity, it is always possible to notice an inertial reference frame in which the particle is stationary with respect to the frame.

Stability [edit]

An of import holding of systems at mechanical equilibrium is their stability.

Potential energy stability test [edit]

If nosotros have a function which describes the system'south potential energy, nosotros can decide the system'southward equilibria using calculus. A system is in mechanical equilibrium at the critical points of the function describing the system's potential energy. We can locate these points using the fact that the derivative of the function is zero at these points. To decide whether or not the system is stable or unstable, we apply the second derivative test. With $V$ denoting the static equation of motion of a system with a single degree of freedom we can perform the following calculations:

Diagram of a brawl placed in an unstable equilibrium.

Second derivative < 0: The potential energy is at a local maximum, which means that the organization is in an unstable equilibrium state. If the system is displaced an arbitrarily small distance from the equilibrium land, the forces of the system cause it to move even farther away.

Diagram of a brawl placed in a stable equilibrium.

Second derivative > 0: The potential free energy is at a local minimum. This is a stable equilibrium. The response to a pocket-size perturbation is forces that tend to restore the equilibrium. If more one stable equilibrium state is possible for a arrangement, whatever equilibria whose potential free energy is college than the accented minimum represent metastable states.

Diagram of a ball placed in a neutral equilibrium.

Second derivative = 0 or does not exist: The land is neutral to the lowest order and about remains in equilibrium if displaced a small corporeality. To investigate the precise stability of the arrangement, higher order derivatives must be examined. The country is unstable if the lowest nonzero derivative is of odd social club or has a negative value, stable if the everyman nonzero derivative is both of even lodge and has a positive value, and neutral if all higher order derivatives are zero. In a truly neutral state the energy does not vary and the state of equilibrium has a finite width. This is sometimes referred to every bit a state that is marginally stable, or in a state of indifference, or astable equilibrium.

When considering more than one dimension, it is possible to go dissimilar results in different directions, for example stability with respect to displacements in the x-direction but instability in the y-direction, a case known as a saddle bespeak. Generally an equilibrium is only referred to as stable if it is stable in all directions.

Statically indeterminate arrangement [edit]

Sometimes there is not enough information about the forces acting on a body to determine if it is in equilibrium or not. This makes it a statically indeterminate system.

Examples [edit]

A stationary object (or set of objects) is in "static equilibrium," which is a special case of mechanical equilibrium. A paperweight on a desk is an example of static equilibrium. Other examples include a rock balance sculpture, or a stack of blocks in the game of Jenga, so long as the sculpture or stack of blocks is not in the state of collapsing.

Objects in motion tin also be in equilibrium. A child sliding down a slide at constant speed would be in mechanical equilibrium, but not in static equilibrium (in the reference frame of the earth or slide).

Some other example of mechanical equilibrium is a person pressing a jump to a defined point. He or she tin can push it to an arbitrary point and hold it at that place, at which betoken the compressive load and the spring reaction are equal. In this state the organization is in mechanical equilibrium. When the compressive force is removed the spring returns to its original state.

The minimal number of static equilibria of homogeneous, convex bodies (when resting under gravity on a horizontal surface) is of special interest. In the planar case, the minimal number is 4, while in 3 dimensions one can build an object with just 1 stable and one unstable residual point.^{[ commendation needed ]} Such an object is called a gömböc.

See too [edit]

Dynamic equilibrium
Engineering science mechanics
Metastability
Statically indeterminate
Statics
Hydrostatic equilibrium

Notes and references [edit]

^ ^a ^b John L Synge & Byron A Griffith (1949). Principles of Mechanics (2nd ed.). McGraw-Colina.
^ ^a ^b Beer FP, Johnston ER, Mazurek DF, Cornell PJ, and Eisenberg, ER (2009). Vector Mechanics for Engineers: Statics and Dynamics (9th ed.). McGraw-Hill. p. 158. {{cite book}}: CS1 maint: multiple names: authors list (link)
^ Herbert Charles Corben & Philip Stehle (1994). Classical Mechanics (Reprint of 1960 second ed.). Courier Dover Publications. p. 113. ISBN0-486-68063-0.
^ Lakshmana C. Rao; J. Lakshminarasimhan; Raju Sethuraman; Srinivasan M. Sivakumar (2004). Engineering Mechanics. PHI Learning Pvt. Ltd. p. half dozen. ISBN81-203-2189-eight.